The 2016 Martin Feldstein Lecture: The Dramatic Economics of the U.S. Market for Higher Education

We have in the United States what is arguably the world's only true market for higher education, as opposed to systems that are largely centrally controlled or financed. This market exhibits a strong positive correlation between students' college readiness (hereafter "CR") and the educational resources of the institution they attend. Moreover, my research shows, the more powerful the market forces, the stronger the correlation.

From my latest research, which breaks new ground with both data and methods, I show the productivity of institutions across this market. Strikingly, among institutions that experience strong market forces, the productivity of a dollar of educational resources is fairly similar, even if the schools serve students with substantially different CR. On the other hand, among institutions that experience weak market forces, productivity is lower and more dispersed. These facts suggest that market forces are needed to keep schools productive and to allocate resources across schools in a way that assures that the marginal return to additional resources at different institutions is roughly comparable.

If we take the productivity results and the resources-CR correlation as manifestations of market forces, then it follows that a student with higher CR must make more productive use of any marginal dollar of educational resources than a student who is less prepared for college. This property, which economists call "single-crossing," has long been hypothesized to be a law of nature, at least in tertiary education. This is the first compelling evidence. Single-crossing has profound consequences for the role of higher education in income growth, a point I clarify when concluding.

The U.S. market for higher education includes about 7,500 institutions. Some are publicly controlled; others are private non-profits or for-profits. Institutions are largely free to decide on pricing (tuition, fees, grants), CR requirements, students, faculty, curriculum, salaries, financial aid, and how to raise money from donors if non-profit or investors if for-profit. Although public schools have less discretion, they still have enormous autonomy by world standards, partly because they are controlled by local and state governments, not a national one, and partly because those governments recognize that public schools must be given latitude if they are to compete with local private schools. Federal intervention is mainly in forms that students can receive regardless of the school they attend: means-tested grants, tax credits and deductions, subsidized loans. On the whole, it is best to think of the U.S. tertiary sector as a market with numerous price distortions relative to laissez-faire, but without central control.¹

U.S. institutions vary enormously in selectivity—that is, in the CR of their students. Selectivity is holistic but, roughly speaking, the "most" selective institutions' average student has a combined (math plus verbal) SAT (or translated ACT) score above 1300, the 90th percentile among test-takers. (Since some students do not take the tests, this corresponds to the 96th percentile among all students.) "Highly" or "very" selective institutions have an average student with combined scores above the 75th percentile (about 1170). "Selective" (without a modifier) institutions ask students to submit scores, grades, and other materials and turn down those judged to be inadequately prepared. Schools with combined scores above 1000 (the 47th percentile) are at least modestly selective. Non-selective schools usually only require that a student have a high school diploma or the equivalent and often have average combined scores of 800 (the 15th percentile) or below. The divide between non-selective and modestly selective schools is rough but somewhere between 800 and 1000.

At its highly selective end, the market is well integrated across geography. Schools compete for students and faculty. Schools are highly informed about their applicants, and students are fairly well informed about schools. High CR students are so valued that they are admitted without regard to their ability to pay, and alumni-donated funds fill the gap between what a student pays and what his education costs.² The high CR students who populate this part of the market make college choices that are elastic with respect to schools' academic and other resources. Such students have strong incentives to internalize the effects of their tertiary education on their future outcomes because they pay for most of their education themselves using family funds or loans they can expect to repay with near certainty. Even alumni-supported grants, which allow lower-income students to attend highly selective schools, generate strong incentives since the schools have every incentive to internalize the effects of educating one generation on their ability to finance the next. (It is worth noting that the market has not always been like this. Rather, the aforementioned features have arisen as information and mobility costs have fallen. I describe the market's evolution in the full-length lecture.³)

At the non-selective end of the market, fairly opposite conditions prevail. Geographic integration, competition, and information are poor. Students, who typically but not universally have low CR, seem not to look outside a set of local schools. Even within this set, they appear insensitive to differences in schools' resources. Because many of these students rely heavily on government funds—including veterans' benefits and loans that will predictably remain unrepaid—their incentives to internalize the effects of their education on their future outcomes is somewhat weak.

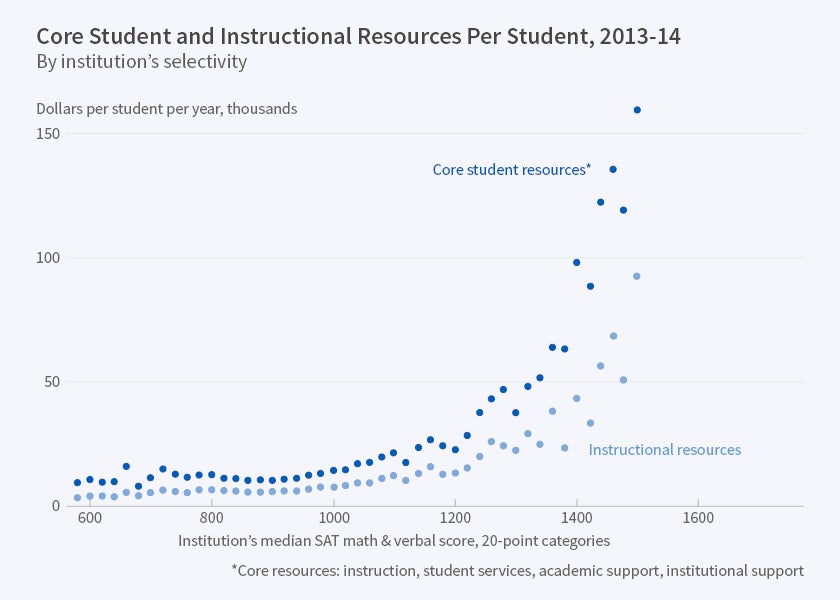
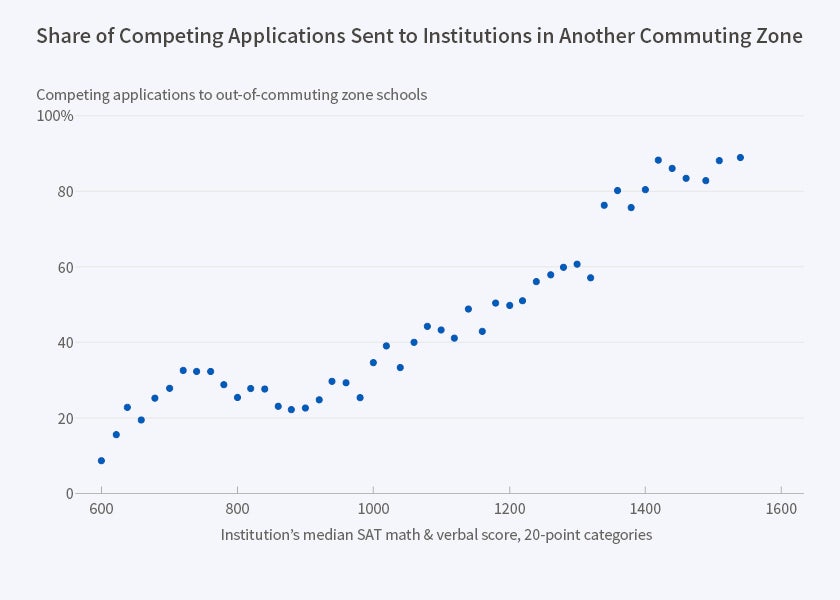
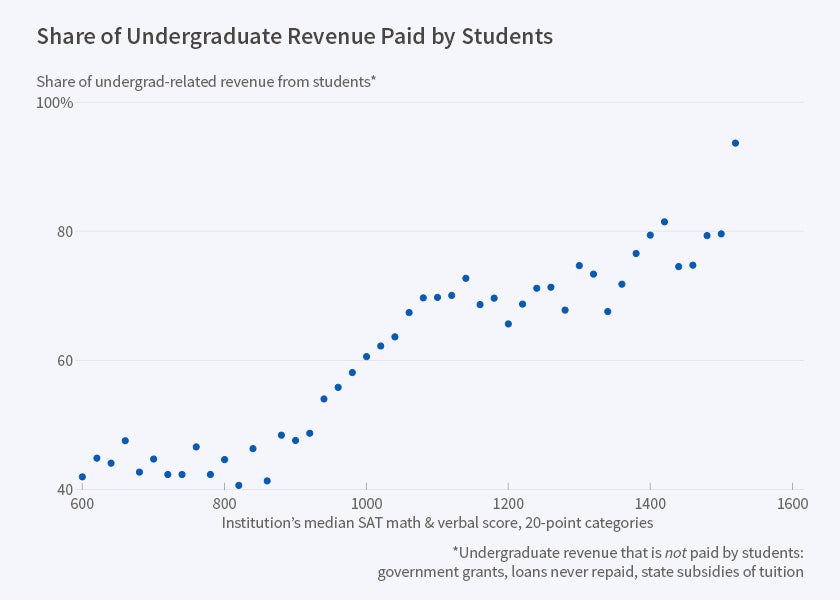
I provide evidence in Figures 1 through 3. Figure 1 shows that the educational resources a student experiences tend to rise monotonically with her CR and that the most selective schools' per-student resources are an order of magnitude greater than those of non-selective schools. Figure 2 shows that nearly all students who apply to a very selective school send most of their (approximately 10) "competing applications" to schools located in a community other than that of the first school. Hardly any applicants to a non-selective school do this, partly because they usually apply to only one school and partly because those who do send multiple applications do so within a small geographic radius. Figure 3 shows that, at non-selective schools, students themselves account for only about 40 percent of undergraduate-related revenue. In contrast, they account for 80 to 95 percent of such revenue at highly selective schools. Information about schools is easily characterized: 100 percent of highly selective schools and about 0 percent of non-selective schools provide comparable information to the common dataset that is used to construct college guides. The availability of information jumps dramatically between non-selective and selective schools.

In short, every indicator—integration, competition, information, financing that generates incentives to internalize consequences—points to market forces being far stronger among highly selective than among non-selective schools.

Measuring the productivity of institutions is crucial if we are to gain a deeper understanding of the market. But producing reliable measures has traditionally been extremely challenging, principally because the strong positive correlation between CR and educational resources generates a formidable selection problem. Do Harvard's graduates have such high lifetime earnings because the school spends so much on their education or because they had such high CR when admitted that they would have had high earnings regardless of their college? To measure productivity, I need data and methods that allow me to deal with selection and estimate a school's value-added, as opposed to the raw outcomes of its graduates. Value-added is the numerator of productivity.

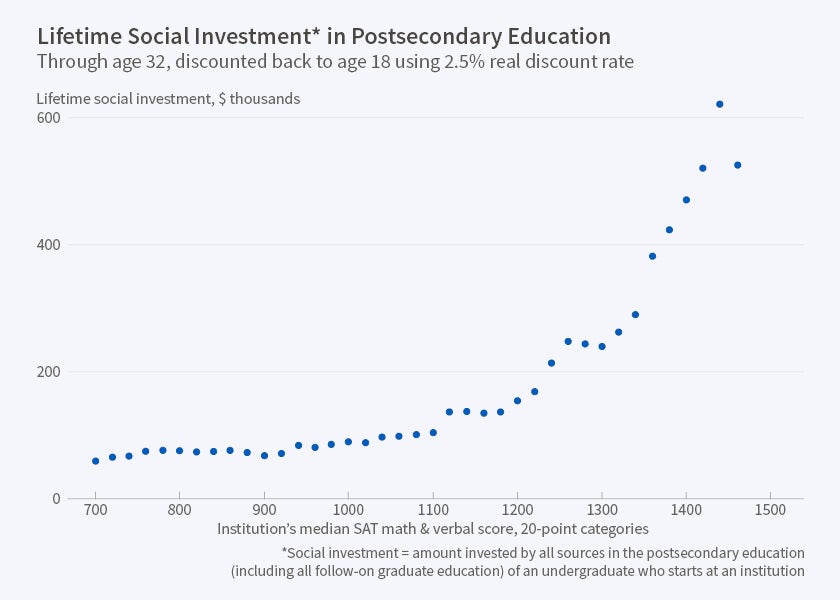
A lesser but still-serious problem plagues the denominator of productivity: the resources devoted to students' education, not only what they spend personally but what society spends in total, including the government and philanthropic funds. I call this "social investment" and it includes not only investment in initial undergraduate schooling but all follow-on education that students are induced to take up. For instance, a Harvard education not only uses more resources (funded by students, donors, and taxpayers) per student each year. Its graduates are more likely to persist as undergraduates and more likely to go to graduate school. Thus, its graduates' lifetime earnings reflect more years, as well as more expensive years, of education. Therefore, individuals' longitudinal educational histories are needed.

My productivity measurements use such histories for virtually all individuals who were in the U.S. during the prime ages for tertiary education—18 to 25—and who were age 32 in 2014. Measurements based on adjacent cohorts are very similar; I use age 32 because it is the earliest age at which one can predict earnings through age 65 well.⁴

I address the selection problem by comparing students who attend different schools but who have identical college assessment scores—indicating extremely similar CR—and who apply to the same schools, thus demonstrating similar taste and motivation. Some of the comparisons are between students who get into two schools of equal selectivity but can choose only one. (From a statistical point of view, it is best if they make such choices "quasi-randomly"—that is, based on some arbitrary factor that matters to them but does not affect long-term outcomes in a significant, consistent way. Examples would be the school's architectural style or the weather on the day they visited.) Other comparisons are between two students who are both "on the bubble" for admission. Admissions staff admit one, quasi-randomly; the other student ends up attending a slightly less selective school. (Admissions staff often make quasi-random decisions. For instance, two students may have equal academic qualifications, but one may be from an area or have an extracurricular interest that would otherwise be underrepresented in the class being admitted.) My procedure combines all of these student-student matchups using paired comparison statistical methods which ensure that the resulting measures rely solely on "apples-to-apples" comparisons (common support, in the language of econometrics). The procedure generates value-added measures for nearly all institutions.

Because there is no broadly applicable way to account for the decision to attend a non-selective post-secondary institution as opposed to common alternatives such as the military and on-the-job training, I do not attempt to compute the value-added of the lowest selectivity schools relative to such alternatives. Instead, I normalize their value-added to zero; it is plausibly greater than or less than zero. It is important to keep this normalization in mind when assessing the figures that follow.

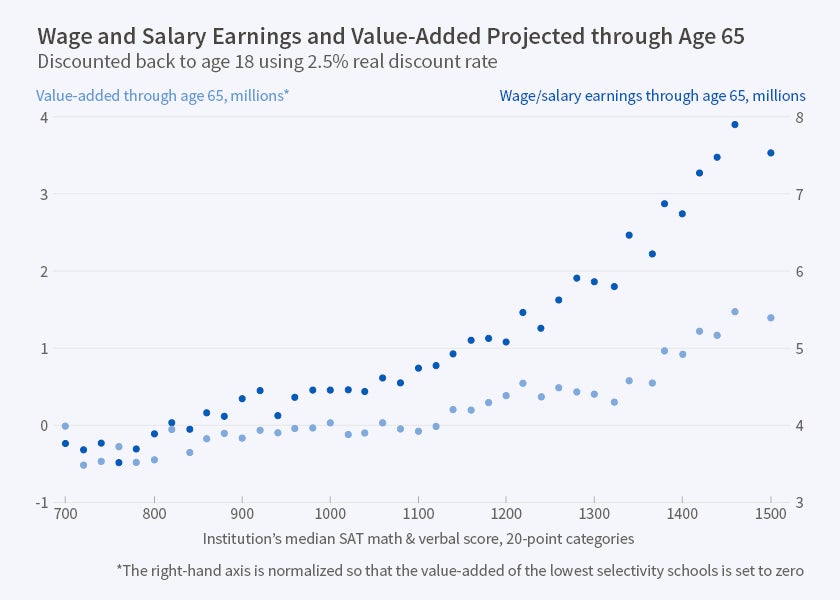
Figure 4 shows value-added versus raw lifetime earnings for nearly all schools, from the non-selective to the most selective. Value-added rises with selectivity, though not nearly as fast as raw earnings. This shows that much of the earnings increase is due to students' higher CR. However, Figure 5 shows that the denominator of productivity, the lifetime educational resources students experience, rises greatly with selectivity. Notice that these resources rise more steeply with selectivity than a single year of resources, shown in Figure 1. This indicates that higher CR students attend more years of higher education.

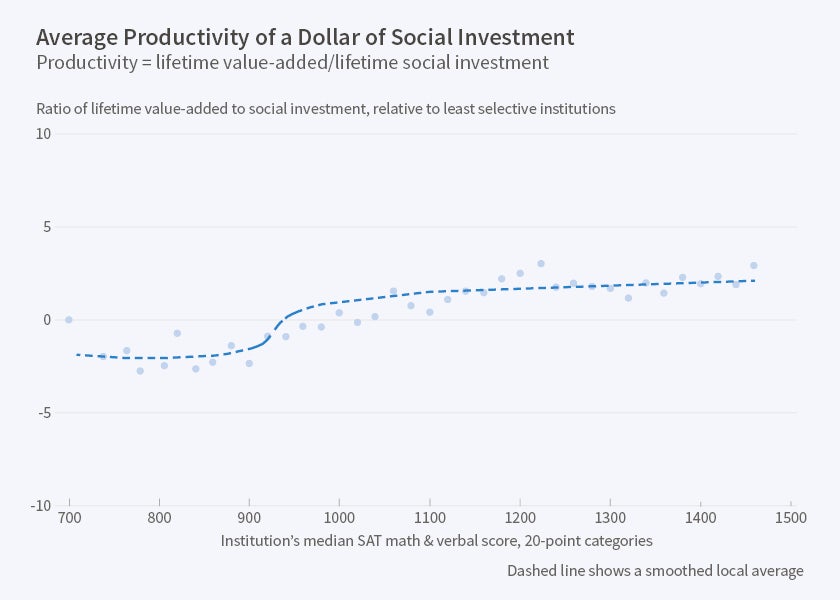
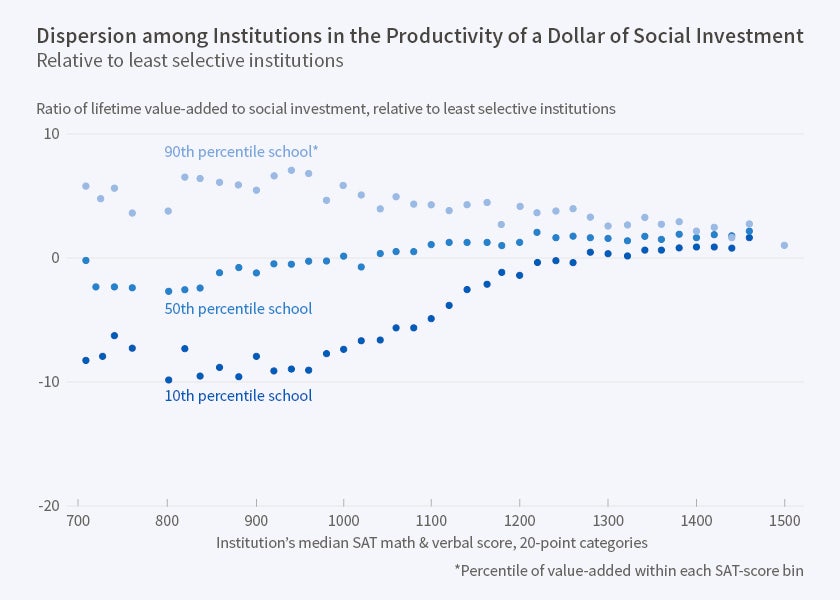
Thus, productivity may rise or fall with selectivity depending on the "race" between its rising numerator and rising denominator. In fact, as shown by Figure 6, the average productivity of a dollar is fairly flat among schools that are selective. There is, however, a notable increase in the level of productivity as we move from the non-selective to selective schools. Figure 7 shows, in addition, that very selective schools whose students have the same CR tend to have similar productivity. In contrast, non-selective schools differ widely in productivity.

The fact that productivity is fairly flat across institutions that range from modestly to highly selective is striking because the least selective schools in this range have much lower educational resources than the most selective schools. Thus, the flat-ness indicates that resources somehow scale up with students' CR so that there would be no easy gains from reallocating dollars among the modestly selective and most selective schools. This is undoubtedly the most important result in this lecture because, when combined with the evidence on market forces, it has profound implications. The evidence in Figure 6 also indicates that the productivity of a dollar at selective institutions is sufficiently positive that they are a good investment for the students who attend them. (For this not to be true, the least selective schools would need to have notably negative value-added instead of the zero to which I have normalized it.) Note that Figure 6 does not imply that selective schools make maximally productive use of resources, just that they make similarly efficient use of resources.

Figure 6 indicates that the average non-selective institution is less productive than selective ones. This result is concerning, especially because enrollment in non-selective schools has grown substantially faster than enrollment in selective schools since at least 1970. The proximate causes of the higher growth rate are fairly clear. The distribution of CR among U.S. secondary school students is largely unchanged since 1970. Thus, selective schools that maintain their CR standards can only grow as fast as the population grows. But non-selective schools grow both with the population and by enrolling students of lower CR — those who would not have been candidates for tertiary education in past years.

As indicated above, it is hard to say whether the average non-selective school is a good investment relative to alternatives like the military or on-the-job training. However, Figure 7 tells us that the average is not of first-order importance anyway. The striking fact is that non-selective schools differ greatly in productivity. This means that students choosing among non-selective schools can make mistakes that have very serious consequences for their life outcomes.

Can economics make sense of all the evidence reviewed so far? Consider a simple world in which (i) there is single-crossing in CR and educational resources; students with higher CR make more productive use of any marginal dollar of resources. Suppose also that (ii) students maximize their return on education; (iii) college choices are not based on geography but, instead, are elastic with respect to schools' resources and outcomes; and (iv) students are fully informed and not liquidity constrained. In this world, market forces would generate an assortatively matched allocation in which higher CR students would be paired with greater educational resources. Crucially, in this world, market forces would require that each dollar of resources be equally productive.

This model, although overly simple, aligns fairly well with what we see in the selective tertiary sector where assumptions (i) through (iv) are not grossly wrong. (It is surprising that the simple model fits as well as it does given that even the selective sector abounds in price distortions, information gaps, and financing problems.) The simple model does not align at all with the non-selective sector, and we should not expect that it would. We have seen evidence that the non-selective sector has little integration, weak competition, poor information, and blunted incentives for participants to internalize the consequences of their educational choices.

What are the broader implications of the evidence and model? If the education production function for tertiary education does indeed exhibit strong single-crossing, they are profound. To make its maximum contribution to economic growth, the higher education sector must allow educational resources to scale up with CR. Yet, the extent of scaling up that occurs in the U.S. is unique. Most countries allocate more, but only modestly more, resources to higher CR students.

Moreover, single-crossing implies that if a country can make all its students attain high CR, it would be growth-maximizing to invest more in the tertiary education of all of them. Educational resources are investments, not consumption, so that, to a first-order, there is nothing zero-sum about them. This key point is often misunderstood: One might incorrectly think that there is a fixed pie of resources so that some students must necessarily get fewer resources if others get more.

Nevertheless, single-crossing in tertiary education puts great pressure on the primary and secondary systems to ensure that all students, regardless of background, are able to attain CR. If educational opportunities are restricted to a subset of students, single-crossing is likely to reduce income mobility and equality. It is important to note that pretertiary education may not exhibit single-crossing just because tertiary education does. Indeed, some economists hypothesize that, in early childhood education, every marginal dollar of resources is more productive for children from more disadvantaged backgrounds.⁵

The other key implication of the evidence and model is that economic growth is likely to increase with policies that facilitate market forces in higher education—better information, greater integration, stronger competition, and financing that makes students and schools internalize the consequences of their choices. Such policies appear to drive educational resources toward a relatively efficient allocation. While we have not seen evidence here that all tertiary education investments earn higher returns than competing uses, such as investments in physical capital, policies that generate greater efficiency within higher education are almost certainly pro-growth.

This is an edited and annotated version of the Martin Feldstein Lecture delivered on July 27, 2016.