The Welfare Effects of Coordinated High School Assignments

A student-matching algorithm derived from economic theory performed better, across a variety of metrics, than the uncoordinated procedure previously used in New York City.

In 2003, about 90,000 incoming high school students in New York City applied for admission to roughly 600 programs of study, offered by some 300 schools. For the first time, the process was mediated through a centralized, coordinated matching algorithm. In The Welfare Effects of Coordinated Assignment: Evidence from the NYC HS Match (NBER Working Paper No. 21046), Atila Abdulkadiroğlu, Nikhil Agarwal, and Parag A. Pathak find that the centralized matching process substantially improved outcomes, measured using several standard metrics, relative to the previous method of school assignment.

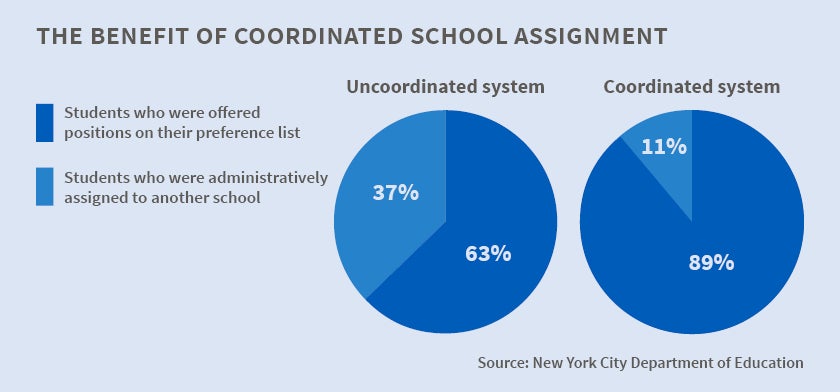
In earlier years, incoming high school students in New York City were matched to programs of study by a complex, uncoordinated procedure. Students ranked their top five programs, and schools observed where students had ranked them. The schools then independently decided which students would be offered admission. There were three rounds of rankings and admissions offers, but this procedure only matched 63 percent of students to schools. The remaining students were administratively assigned to the nearest school to their homes. Many students found the outcomes unsatisfactory, and 8.5 percent of students left the New York school district after receiving their school assignment. Further, some schools advertised they were only interested in students who ranked them first, encouraging some students to strategically misrepresent their preferences.

For the school year 2003-04, this matching process was substantially altered. Students were asked to rank their top 12 programs, and schools coordinated with one another in making offers of admission. This process was based on a matching algorithm designed by mathematicians David Gale and Lloyd Shapley, winner of the 2012 Nobel Prize in Economics. Unlike the previous matching mechanism, the Gale-Shapley algorithm encourages students to report their preferences truthfully. Further, it matches as many students as possible and creates stable matches. Though students are not guaranteed their top choices, there are never any vacancies at a school that any student ranked higher than the one to which he or she was assigned. The algorithm was used for two rounds of assignments; those students who did not match in either round were assigned administratively.

The new algorithm performed better than the old, uncoordinated mechanism by reducing exits from the schools and the number of students administratively assigned. With the new algorithm, only 6.4 percent of students left the district after receiving a school assignment. Moreover, despite having fewer rounds of matching, the new mechanism ended up matching 89 percent of students before resorting to administrative assignment. The authors also develop a statistical model that predicts how much a given student will like a given school based on both student and school characteristics. It suggests that the matching algorithm significantly improved overall welfare, with the largest gains for those students no longer matched via administrative assignment to the nearest school. Because fewer students were in this category, the new algorithm sent the average student to a school 20 percent (0.7 miles) farther from his or her home. Nonetheless, the authors estimate that the improved school match more than compensated for the extra distance.

-- Andrew Whitten